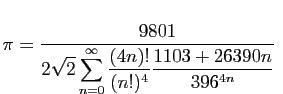Srinivasa Ramanujan, autodidacte et génie des mathématiques

Mes chers amis, dans ce nouveau thème et le premier consacré aux mathématiques, je vais revenir sur l'incroyable histoire du mathématicien indien Srinivasa Ramanujan (1887-1920) un des plus grands génies du XXe siècle.  Ses travaux dans le domaine des mathématiques  ont apporté énormément tant dans le développement de formules que dans la démonstration analytique . Le mathématicien qui grace à une capacité extraordinaire, liée à la virtuosité grandiose a permis de développer de nombreuses formules indispensables quand à la compréhension de nombreux phénomènes. Il est d'ailleurs le créateur de plusieurs milliers de formules et théorèmes. Génie au talent exceptionnel il est totalement autodidacte, et pour cause il apprend seul les mathématiques grace à seulement deux ouvrages !  Avant l'age de 16 ans la lecture seule de ces ouvrages dont A Synopsis of Elementary Results in Pure and Applied Mathematics de George S Carr. va lui permettre d'acquérir une conscience mathématique, cela combiné à un potentiel prodigieux lui donnent la possibilité quelques années plus tard de réflechir sur de nombreux domaines des mathématiques comme notamment sur la théorie des nombres,  ou sur les séries divergentes, sans oublier son raisonnement autour du nombre Pi et de ses décimales pour laquel il est assez célèbre. De formation indépendante, Il est l'auteur de plusieurs articles dans des journaux indiens , mais espère de pouvoir intéresser l'europe et ses mathématiciens reconnus autour des ces découvertes inédites, ce qui lui donnera cette reconnaissance tant attendue... Pour ce faire il tente de faire connaitre ses travaux, en envoyant des lettres à des sommités des mathématiques, mais c'est ses echanges épistolaires a partir de l'année 1913 avec le grand mathématicien britannique Godfrey Harold Hardy ( 1877-1947) qui lui donnent l'opportunité historique de faire connaitre son travail remarquable et sa poèsie des nombres.

La fabuleuse révélation du mathématicien indien

Srinivasa Ramajuan se familiarise également à l'age de 17 ans aux nombres du mathématicien Jacques Bernoulli (1654-1705). Le génie indien va s'interesser de près à cette suite de nombre rationnels. Mes chers amis je vous rappelle qu'un nombre rationnel en mathématiques est un nombre qui peut s'exprimer comme le quotient de deux entiers relatifs ou plus simplement de deux nombres entiers. L'obsession du génie autodidacte pour les mathématiques le fait paraitre comme un elève médiocre dans dans d'autres domaines comme la biologie et de ce fait il perd sa bourse . En 1906 et 1907 il échoue à un examen qui aurait pu lui apporter une autre vision à cette époque, ce qui le contraint à renoncer à un cursus classique , néanmois il continue ses travaux sur les nombres. Durant cette période compliquée pour lui il doit affrontrer deux ecceuils importants : une grande pauvreté  et un isolement social.Conséquence directe de cette situation la naissance de son propre système de notation, la rédaction de ces fameux cahiers et surement de sa capacité extraordinaire en mathématiques.

Premières contributions mathématiques et correspondance avec des mathématiciens de l'université de Cambridge

En 1912 aidé par le mathématicien britannique Edgar William Middlemast ( 1864 - 1915) Srinivasa Ramajuan commence sa correspondance et tente de prendre contact avec des mathématiciens britanniques d'abord de l'université de Londres comme  Micaiah John Muller Hill ( 1856-1929) sans grand succès en cause certaines lacunes et un manque de clarté. L'ironie du sort est que justement  les travaux du professeur Hill sont davantage connus grace à la célèbrité du mathématicien indien. N'obtenant pas le succès escompté , il va essayer de convaincre les mathématiciens les plus prestigieux de l'université de Cambridge, il se lance donc dans l'ecriture de lettres. Une date fatidique dans la vie du génie indien : le 16 janvier 1913 il envoie une lettre de plus de neuf pages au mathématicien britannique Godfrey Harold Hardy. Suite à la reception de cette lettre, le professeur Hardy se montre très impressionné par les capacités extraordinaires du mathématicien indien, d'ailleurs certaines formules lui semble  assez surréalistes, tellement rares et uniques qu'il pense au début à un canular. Mais le pragmatisme retrouvé, il demande au mathématicien John Edensor Littlewood (1885-1977) de lire la lettre contenant les fameuses formules, ce dernier se montre stupéfait quand à l'analyse de ces ecritures mathématiques, il va jusqu'a qualifier Srivinasa Ramanujan "d'homme de génie".

Le 8 fevrier 1913, le mathématicien indien recoit une réponse positive, ou Hardy reconnait la qualité de son travail et en son for intérieur il souhaite que Ramanujan vienne à Cambridge expliquer ses travaux et pouvoir collaborer avec d'autres mathématiciens qui pourront peut etre lui apporter l'esthétique liée à la presentation de ses formules et calculs qui a pu lui faire défaut. Godfrey Harold Hardy cherchant à organiser le sejour du génie autodidacte an Angleterre prend contact avec le bureau de l'inde, cette instance officielle en lien avec l'exécutif britannique tente de convaincre Ramanujan mais rencontre un premier refus et pour cause il s'oppose à ce départ en europe pour respecter ses croyances brahmanes et également de respecter la tradition familiale indienne. Mais tout change quand il recoit la bénédiction de sa mère qui aurait apercu la déése indienne Namagiri Thayar dans son rève lui ordonnant de laisser son fils vivre sa vie.

Voyage en Angleterre, reconnaissance posthume et apports théoriques dans le domaine des mathématiques 

Cette opposition profonde sera à l'origine d'une toute nouvelle interprétation des mathématiques en occident et dans le monde. L'intuition prodigieuse et liée à la fulgurance tandis que Hardy est d'avantage dans une méthodologie analytique, alliée à une approche classique et détaillée. Néanmois la capacité extraodinaire du prodige indien continue d'impressionner le professeur britannique, par son coté prolifique et par la grande cohérence et maitrise déployée pour parvenir aux résultats. Srinivasa Ramanujan passera plus de 5 ans a Cambridge en Angleterre à presenter tout son talent et ses formules mathématiques...  Le 6 décembre 1917 il recoit son admission à la London mathématical sociéty, et l'année suivante il est élu Fellow of the Royal Sociéty, cette société savant prestigieuse qui a compté dans ses rangs le philosophe Robert Boyle ( 1627-1691) ou encore le mathématicien légendaire Isaac Newton ( 1642-1727).

Mais le prodige indien va malheureusement souffir de problèmes de santé durant toute son éxistence, de plus la première guerre mondiale de par ses restrictions n'arrange rien à l'affaire, et la santé de Ramanujan se dégrade assez rapidement en partie du à a son régime végetarien...  Dépité et ne voyant pas de solutions, Il tente de se suicider en 1918. La fin de la première guerre mondiale lui permet de repartir dans son pays natal, et en mars 1919 il retourne dans la province de Madras, mais malheuresement son rétablissement est juste temporaire, et son état de santé s'empire dangereusement, tres fatigué et a bout de souffle, il décède le 26 avril 1919, agé de 32 ans.

Cahiers de Ramanujan,  Le Nombre Pi, formules et théorèmes

Les cahiers de Srinivasa Ramanujan, des manuscrits très importants contenant des milliers de formules mathématiques  il en existe trois à l'origine et un quatrième qui a été retrouvé en 1976. Ces receuils de calculs avec le légendaire style elliptique du prodige indien sont toujours à l'étude... Ils contiennent encore de très nombreux mystères. La qualité de ces travaux est incroyable, avec une très grande partie de résultats exacts. Le mathématicien indien est également connu pour ses découvertes majeures au sujet du Nombre Pi (3,141592), en effet l'etude de ce nombre le passionne et en 1910 il découvre un ensemble de formules dont la principale n'a été démontréé qu'en 1985 ! Le mathématicien indien symbolise une exception au sens historique du terme avec des intuitions fulgurantes et mystèrieuses.

Formule de Srinivasa Ramanujan datant de 1910 et permettant de calculer le nombre Pi avec 17 millions de décimales